Классическая динамика живого.
19 декабря 2008 года.
Басина
Г. И.
Проф. Басин
М. А.
Научно-исследовательский
центр «Синергетика»
Санкт-Петербургского
союза учёных.
E-mail: basin@soft-tronik.spb.ru
Столетнему
юбилею выдающегося учёного, профессора Басина, Абрама Моисеевича, посвящается.
Одними из основных свойств живых
объектов являются их рост и размножение, тесно связанные между собой. Так,
например, рост клеток соответствует размножению органических веществ клетки,
рост организма соответствует серии процессов деления клеток с последующим их
ростом, рост популяции организмов (рост массы вида) определяется
последовательным размножением и ростом живых организмов. В живой природе, так
же как и в неживой, параметром целого, то есть параметром (мерой), интегрально
характеризующей биологический объект как целостную структуру или систему,
является его масса, которая на каждом уровне биологической иерархии может быть
связана с числом элементов (квантов), входящих в этот объект как в обобщённую
волну [1]-[5].
Для математического описания
размножения и роста живых объектов: клеток, организмов, популяций, человека и
человеческого общества, - используют автономные дифференциальные уравнения типа:
, (1)
где
- некоторая мера
(параметр целого), приближённо характеризующая число клеток в организме, число
организмов в популяции или массу клетки, организма, популяции [3]-[16]. Однако
применимость уравнения (1) значительно шире, оно может быть использовано для
описания любого переходного процесса. Так, например, в монографиях [17] - [18] его
частный случай, логистическое уравнение, использовано для анализа динамики Internet.
В настоящей статье мы покажем, следуя [19],
что уравнение (1) формально эквивалентно уравнению динамики одномерного
движения ньютоновой точки в потенциальном поле, а роль пространственной координаты
в этом случае играет величина .
Произведём
следующие преобразования. Продифференцируем обе части уравнения (1) по времени 
:
. (2)
Используя
уравнение (1), получаем:
. (3)
Введя
обозначение
, (4)
получаем
. (5)
Уравнение
(5) является полным аналогом уравнения одномерного движения изолированной точки
в потенциальном поле. Мера - аналог координаты точки, а функция 
- аналог механической
силы, действующей на точку.
Далее выполним следующие
преобразования, которые позволят построить для живого объекта аналог
кинетической и потенциальной энергии и вывести закон сохранения «энергии» для растущих и
размножающихся живых организмов.
Умножим обе части
уравнения (5) на одну и ту же функцию 
. (6)
Умножение
левой и правой частей уравнения (6) на 
даёт следующее
соотношение:
.
(7)
Интегрируя
левую и правую части уравнения (7), получаем:
(8)
Введём
обозначение:
(9)
и
назовём величину 
кинетической энергией
роста (размножения) живых объектов. Правая часть уравнения (8) является только
функцией от . Величина 
может быть однозначно
определена, если учесть уравнение (1). Подставляем в (8) выражение (4)
. (10)
Или
.
(11)
Из
(1) следует равенство
. (12)
Откуда
имеем
. (13)
Преобразуем
уравнение (12)
.
(14)
Функцию
обозначим через 
и назовём
потенциальной энергией роста и размножения.
Уравнение
(14) может быть записано в виде закона сохранения суммарной энергии роста или размножения.
. (15)
Введём
в рассмотрение функцию Гамильтона
(16)
Величина
функции 
остаётся постоянной и равной 
в процессе роста и
размножения клеток организма или элементов в популяции. Эту величину можно
назвать полной энергией роста биологического объекта или размножения биологических
объектов. Из равенств (16) и (1) получается система уравнений Гамильтона
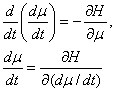. (17)
Величина
является аналогом
механической скорости и количества движения при одномерном механическом
движении и может быть названа биологическим импульсом, тогда как сама величина - биологической координатой.
Однако, несмотря на внешне полное
формальное соответствие полученных формул формулам классической механики, в
действительности между ними существуют принципиальные отличия. Эти отличия
связаны с тем, что кроме системы уравнений (16), (17) существует ещё уравнение
(1), накладывающее дополнительное ограничение на скорость роста, которое
исключает классическую обратимость движения. Каждой паре значений полной
энергии 
и координаты соответствует лишь одно значение скорости (импульса) роста , а не два значения противоположного знака как в классической
механике. Тем самым полученные формулы уже не описывают обратимое движение, как
это происходит при использовании аналогичных формул в классической механике.
Движение происходит только в одну сторону, и его направление описывается
уравнением (1). Кроме того, сама величина может быть только
положительной, что накладывает дополнительные ограничения на применимость решений
полученных уравнений.
Приведём два примера.
1.
Рассмотрим непрерывную модель простого размножения. В этом случае функция 
принимает вид:
, (18)
а
уравнение (1) приобретает следующую форму:
(19)
Уравнение
(3) преобразуется к виду:
. (20)
Потенциальная
энергия простого размножения определяется формулой
, (21)
а
функция Гамильтона имеет вид:
. (22)
В
процессе роста популяции (размножения клеток) величина остаётся постоянной и выполняется равенство:
. (23)
Величина
, в принципе, может быть принята произвольной. Некоторые
дополнительные соображения позволяют сделать её выбор более определённым. Если
предположить, что в начальный момент времени параметр целого системы очень мал, то его в
первом приближении можно принять равным нулю. К нулю также стремится и
«кинетическая энергия». Биологическая потенциальная энергия при этом стремится
к максимальному значению
.
(24)
При
простом размножении клеток число клеток или их масса могут увеличиваться
неограниченно. Следовательно, неограниченно будет расти кинетическая энергия и
падать потенциальная энергия роста организма. Если принять условие, что простое
размножение может продолжаться неограниченно долго и потенциальная энергия не может
стать меньше нуля, то в начальный период движения величина потенциальной
энергии, а следовательно, и величина стремится к
бесконечности. То есть потенциальная энергия простого размножения
асимптотически бесконечна. В действительности, модель, описываемая уравнением
(20), является лишь асимптотическим приближением реальных процессов роста и
размножения организмов, которые обязательно замедляются или прекращаются по тем
или иным причинам. И выбор величины зависит от внешних по
отношению к этой асимптотике условий, например, из условия равенства нулю
потенциальной энергии в точке её минимума. Однако, рассмотренный нами парадокс
свидетельствует об одном очень важном свойстве живого – очень большом
(возможно, практически неограниченном) потенциале роста и размножения живой
материи.
При описании роста реальных популяций и
в ряде других случаев используется
модель логистического уравнения [17-18], [20]
.
(25)
Фазовая
плоскость этого уравнения имеет две стационарные точки
. (26)
Продифференцируем обе части
уравнения (25) по времени
.
(27)
Ускорение
роста равно нулю в трёх точках биологического пространства,
. (28)
В
точке 
скорость роста (биологическое количество
движения) принимает максимальное значение
. (29)
Потенциальная
энергия размножения (роста) имеет вид
. (30)
В
точке кинетическая энергия роста максимальна
, (31)
а
потенциальная энергия роста минимальна
. (32)
Её
значение в этой точке можно принять равным нулю. Тогда однозначно определяется
величина , а вместе с ней величина суммарной биологической энергии
(гамильтониана)
. (33)
Окончательная
формула для потенциальной энергии роста:
. (34)
Если
рассмотреть зависимость потенциальной энергии от величины , то при 
потенциальная энергия
роста стремится к своему максимальному значению. С увеличением величины растет кинетическая
энергия роста (размножения), которая достигает максимума при ,
потенциальная энергия при этом равна нулю. Затем кинетическая энергия начинает
уменьшаться и стремится к нулю при
. При этом потенциальная энергия вновь стремится к своему
максимальному значению. Однако, в отличие от классической механики, возвратное
движение, в рамках рассматриваемой модели вследствие справедливости уравнения
(1) невозможно.
Реально происходит следующее. Биологический
организм асимптотически стремится к состоянию, соответствующему максимуму
величины (). Теоретически, как следует из решения уравнения (25), это
происходит через бесконечный промежуток времени. Практически со временем
«стареет» структура, обеспечивающая основные свойства живого организма и через
некоторый конечный промежуток времени организм разрушается. Этот процесс
требует дополнительных математических моделей и специального теоретического
исследования. Однако, если бы дело было только в этом, то жизнь, однажды
начавшись вскоре бы закончилась. Оказывается, что живые организмы, во всяком
случае, высшие, несут в себе ещё один потенциал, в чём-то аналогичный
электрическому - потенциал полового размножения. Не останавливаясь на его
деталях, обратим внимание лишь на то, что в результате действия этого механизма
появляются новые биологические объекты, аналогичные первоначальному, которые
имеют начальные значения параметра целого, стремящиеся к нулю, и вновь
повторяют путь, пройденный первоначальным организмом. Формируется нелинейная
циклическая динамика, однако каждый новый цикл проходит обновлённый организм,
информационно (генетически) связанный с предыдущим. При этом старый организм в
это же время может продолжить своё существование, следствием чего является
формирование популяции организмов, динамика которой также может быть описана
дифференциальным уравнением первого порядка, но функция имеет другой вид [5],
[6], [9-13], [15], [16].
Уравнение (25) также может быть
применено к описанию динамики роста отдельной клетки. Однако, динамика роста начинается
в этом случае с точки, соответствующей максимуму кинетической энергии и нулевой
потенциальной энергии. Затем рост массы клетки соответствует уменьшению до нуля
кинетической энергии и достижению потенциальной энергией своего максимального
значения. Вблизи этого состояния происходит потеря устойчивости и деление
клетки, возвращающее обе получившиеся половинки в состояние, соответствующее
начальному состоянию материнской клетки. Как и в случае организма, формируется
два процесса: нелинейный циклический процесс для отдельной клетки и процесс
простого размножения для популяции клеток. Энергия динамики роста и размножения
клеток коррелирует с энергией простого размножения популяции клеток
Таким образом, динамика роста и
размножения живых организмов может рассматриваться как специфический случай
гамильтоновой динамики, в которой роль обобщённых координат играют параметр
целого биологической системы и его производная по времени. Полезным оказывается
введение биологических импульса, силы, кинетической, потенциальной и полной
энергии.
Литература.
1.
Синергетика и методы науки. СПб.: Под ред. М. А. Басина. Л.: Наука. 1998. 439 с.
2.
Басин М. А. Волновой подход к исследованию структур и систем //. Реальность и
субъект. Т. 2. №№ 2-3. СПб.: 1998. С. 57-72.
3.
Басин М. А. Волны. Кванты. События. Волновая теория взаимодействия структур и
систем. Часть 1. СПб.: Норма. 2000. 168 с.
4.
Басин М. А. Компьютеры. Вихри. Резонансы. Волновая теория взаимодействия
структур и систем. Часть 2. СПб.: Норма. 2002. 144 с.
5.
Басин М. А. Человек и человечество. Некоторые нестандартные модели // Реальность
и Субъект. Т. 6. №1. СПб.: 2002. С. 33-43.
6.
Басина Г. И., Басин М. А. Синергетика. Эволюция и ритмы человечества. СПб.:
Норма. 2003. 260 с.
7.
Басина Г. И., Басин М. А. Синергетика. Основы методологии. СПб.: Норма. 2006. 56.с.
8.
Басина Г. И., Басин М. А. Синергетика. Вселенная резонансов. СПб: Норма. 2008.
144 с.
9.
Капица С. П. Математическая модель роста населения мира // Математическое
моделирование. 1992. Т. 4. № 6.
10.
Капица С. П., Курдюмов С. П. Малинецкий Г. Г. Синергетика и прогнозы будущего.
М.: 1977.
11.
Капица С. П. Синергетика и демография // Сборник, посвящённый 70 летию С. П.
Курдюмова. М.: 1998.
12.
Капица С. П. Общая теория роста человечества. Сколько людей жил, живёт и будет
жить на Земле.М.: Наука. 1999. 199 с.
13.
Капица С. П. Мировой демографический кризис и Россия. // Будущее России. Вызовы
и проекты: История. Демография. Наука. Оборона. / Под ред. Г. Г. Малинецкого.
М.: Издательство ЛКИ. 2008 С. 71 - 88.
14.
Солбриг О., Солбриг Д. Популяционная биология и эволюция. М.: Мир. 1982 с.
15.Подлазов
А. В. Теоретическая демография. Модели роста народонаселения и глобального
демографического перехода// Новое в синергетике. Взгляд в третье тысячелетие. (Информатика:
неограниченные возможности и возможные ограничения) М.: 2002. С. 334-345.
16.
Баранцев Р. Г. Синергетика в современном естествознании. М.: Едиториал УРРС. 2003.
144 с.
17.
Басин М. А. Шилович И. И. Синергетика и Internet.
(Путь к Synergonet) СПб.: Наука. 1999. 71 с.
18.
Басин М. А. Шилович И. И. Путь в Synergonet СПб.: Норма. 2004. 128 с.
19.
Арнольд В. И. Математические методы классической механики. Главная редакция
физико - математической литературы изд-ва «Наука». 1974. 432 с.
20.
Арнольд В. И. Обыкновенные дифференциальные уравнения. М.: Наука. 1971. 240 с.